Question

2. Elena finds that the area of a house on a scale drawing is 25 square inches. The

actual area of the house is 2,025 square feet. What is the scale of the drawing?

Answer 1

9

Explanation:

Answer 2

The scale of the drawing is
`(1)/(9)\ (in)/(ft)`

Explanation:

we know that

If two figures are similar, then the ratio of its areas is equal to the scale factor squared

Let

z ----> the scale factor

x ----> the area of an house on a scale drawing in square inches

y ---> the actual area of the house in square feet

`z^2=(x)/(y)`

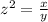
we have

`x=25\ in^2`

`y=2,025\ ft^2`

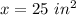
substitute

`z^2=(25)/(2,025)`

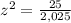
simplify

`z^2=(1)/(81)`

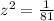
square root both sides

`z=(1)/(9)\ (in)/(ft)`

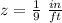
therefore

The scale of the drawing is
`(1)/(9)\ (in)/(ft)`