Question

Kyra has a rock collection. When she puts her rocks into 2 equal plies, there are no rocks left over. When she puts her rocks into 3 equal piles, there are still no rocks left over. When she puts her rock into 4 equal piles, there are still no rock left over. How many rocks could kyra have?

Answer 1

Explanation:

According to this description we need a number that can be divided by 2,3 and 4 since the amount of rocks can be described by a natural number. However if a number is divided by 4 it is divided by 2 as well since 2*2=4.

`(x)/(4) = \alpha \\ (x)/(2) = 2 \alpha`

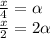
If α is a natural number then 2*α is a natural number as well as the product of two natural numbers.

Which means that we need a number devided by 3 and 4.

The smallest number that fulfills this demand is 3*4=12.

Also any product of 12 with any natural number can be devided by 3, 4 and 2.

If the exercise asks for the numbers that are divided only by 2,3 and 4 these are:

`{3}^( \alpha ) * 12 \: and \: {4}^( \alpha ) * 12 \: \\ where \: \alpha \: belongs \: to \: the \: set \: of \: all \: </p><p>\\ natural \: numbers`