Answer:
Total Distance = 2 miles
Explanation:
We know D = RT where
D is distance
R is rate (speed)
T is time
First Leg:
Rate = x mph
Time = 20/60 = 1/3 hour
Hence, D = RT, Distance = x * 1/3 = x/3 miles
Second Leg:
Rate = x - 1
Time = 30/60 = 1/2 hour
Distance = (x - 1) * 1/2 = (x-1)/2
Total distance is the sum of both the legs, hence,
Total distance =
 miles
miles
Since both the distance are equal we can equate and solve:
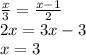
Plugging this x = 3 into the total distance expression, we get:

Total distance, 2 miles