Answer:
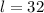 and
and

Explanation:
Given: The length of a rectangle is eight more than twice its width. The perimeter is 88 feet.
To find: The dimensions of the rectangle.
Solution:
It is given that the length of a rectangle is eight more than twice its width.
Let the width of the rectangle be w.
So, the length of the rectangle
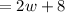
We know that the perimeter of a rectangle is
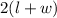
Here, perimeter of rectangle

So, we have
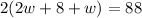

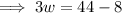
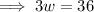
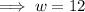
Therefore, width of the rectangle is 12 feet
length
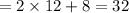
Hence, length of the rectangle is 32 feet and width of the rectangle is 12 feet.