Question

A rectangular schoolyard is to be fenced in using the wall of the school for one side and 150meters of fencing for the other three sides. The area A(x) in square meters of the schoolyard is afunction of the length I in meters of each of the sides perpendicular to the school wall1. Write an expression for A(x)2. What is the area of the schoolyard when x=40?3. What is a reasonable domain for A in this context?​

Answer 1

Part 1) The expression is
`A(x)=150x-2x^2`

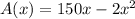
Part 2) The area of the schoolyard when x=40 m is A=2,800 m^2

Part 3) The domain is all real numbers greater than zero and less than 75 meters

Explanation:

Part 1) Write an expression for A(x)

Let

x -----> the length of the rectangular schoolyard

y ---> the width of the rectangular schoolyard

we know that

The perimeter of the fencing (using the wall of the school for one side) is

`P=2x+y`

`P=150\ m`

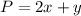
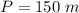
so

`150=2x+y`

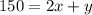
`y=150-2x` -----> equation A

The area of the rectangular schoolyard is

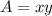`A=xy` ----> equation B

substitute equation A in equation B

`A=x(150-2x)`

`A=150x-2x^2`

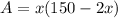
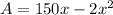
Convert to function notation

`A(x)=150x-2x^2`

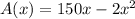
Part 2) What is the area of the schoolyard when x=40?

For x=40 m

substitute in the expression of Part 1) and solve for A

`A(40)=150(40)-2(40^2)`

`A(40)=2,800\ m^2)`

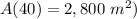
Part 3) What is a reasonable domain for A(x) in this context

we know that

A represent the area of the rectangular schoolyard

x represent the length of of the rectangular schoolyard

we have

`A(x)=150x-2x^2`

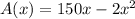
This is a vertical parabola open downward

The vertex is a maximum

The x-coordinate of the vertex represent the length for the maximum area

The y-coordinate of the vertex represent the maximum area

The vertex is the point (37.5, 2812.5)

see the attached figure

therefore

The maximum area is 2,812.5 m^2

The x-intercepts are x=0 m and x=75 m

The domain for A is the interval -----> (0, 75)

All real numbers greater than zero and less than 75 meters