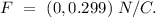Question

Two point charges are placed on the x axis.The firstcharge, q1= 8.00 nC, is placed a distance 16.0 mfromthe origin along the positive x axis; the second charge,q2= 6.00 nC, is placed a distance 9.00 mfrom the originalong the negative x axis.[Give the x and y components of the electric fieldas an ordered pair. Express your answer innewtons per coulomb to three significant figures.Keep in mind that an x component that points tothe right is positive and a y component thatpoints upward is positive.]

Answer 1

E = (0, 0.299) N

Step-by-step explanation:

Given,

• Charge
  `q_1\ =\ 8.0\ nC`
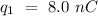
• Charge
  `q_2\ =\ 6.0\ nC`
• Distance of the first charge from the origin = (16m, 0)
• Distance of the second charge from the origin = (-9, 0)
• Point where the electric field required = (0, 12m)

Let
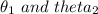`\theta_1\ and\ theta_2` be the angle of the electric fields by first and second charge at the point A.

`\therefore sin\theta_1\ =\ (12)/(20)\\\Rightarrow \theta_1\ =\ sin^(-1)\left ((12)/(20)\ \right )\\\Rightarrow \theta_1\ =\ 36.87^o\\\\\therefore sin\theta_1\ =\ (12)/(9)\\\Rightarrow \theta_1\ =\ sin^(-1)\left ((12)/(9)\ \right )\\\Rightarrow \theta_1\ =\ 53.13^o\\`

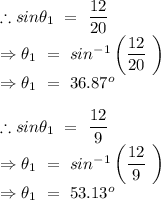
Electric field by charge
`q_1` at point A,

`F_1\ =\ (kq_1)/(r_1^2)\\\Rightarrow F_1\ =\ (9* 10^9* 8* 10^(-9))/(20^2)\\\Rightarrow F_1\ =\ 0.18\ N/C`

Electric field by the charge
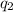`q_2` at point A,

`F_1\ =\ (kq_1)/(r_1^2)\\\Rightarrow F_1\ =\ (9* 10^9* 6.0* 10^(-9))/(16^2)\\\Rightarrow F_1\ =\ 0.24\ N/C`

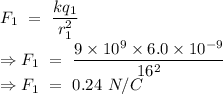
Now,

Net electric field in horizontal direction at point A
`F_x\ =\ F_(1x)\ +\ F_(2x)\\\Rightarrow F_x\ =\ F_1cos\theta_1\ +\ F_2cos\theta_2\\\Rightarrow F_x\ =\ 0.18*( -cos36.87^o)\ +\ 0.24* cos53.13^o\\\Rightarrow F_x\ =\ -0.144\ +\ 0.144\ N/C\\\Rightarrow F_x\ =\ 0\ N/C`

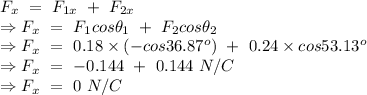
Net electric field in vertical direction at point A.

`F_y\ =\ F_(1y)\ +\ F_(2y)\\\Rightarrow F_y\ =\ F_1sin\theta_1\ +\ F_2sin\theta_2\\\Rightarrow F_y\ =\ 0.18* sin36.87^o\ +\ 0.24* sin53.13^o\\\Rightarrow F_y\ =\ 0.180\ +\ 0.192\\\Rightarrow F_y\ =\ 0.299\ N/C`

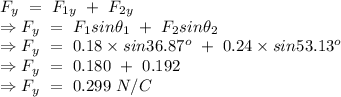
Hence, the net electric field at point A,

`F\ =\ ( 0, 0.299 )\ N/C.`