Question

Air at 30°C and 2MPa flows at steady state in a horizontal pipeline with a velocity of 25 m/s. It passes through a throttle valve where the pressure is reduced to 0.3 MPa. The pipe is the same diameter upstream and downstream of the valve. What is the outlet temperature and velocity of the gas? Assume air is an ideal gas with a temperature-independent CP  7R/2, and the average molecular weight of air is 28.8.

Answer 1

`V_2=159.9\ m/s`

`T_2=290.6K`

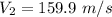
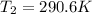
Step-by-step explanation:

At initial condition

P=2 MPa

T=30°C

V=25 m/s

At final condition

P=0.3 MPa

Now from first law for open system

`h_1+(V_1^2)/(2000)=h_2+(V_2^2)/(2000)`

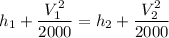
We know that for air

h= 1.010 x T KJ/kg

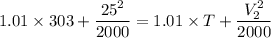`1.01* 303+(25^2)/(2000)=1.01* T+(V_2^2)/(2000)` -----1

Now from mass balance

`\rho_1A_1V_1=\rho_2A_2V_2`

We also know that

`\rho=(P)/(RT)`

`(P_1)/(RT_1)V_1=(P_2)/(RT_2)V_2`

`(2)/(R* 303)* 25=(0.3)/(RT_2)V_2`

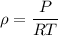
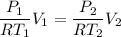
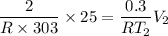
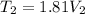`T_2=1.81V_2` ----------2

Now from equation 1 and 2

`V_2^2+3673.749V-612916.49=0`

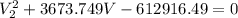
So we can say that

`V_2=159.9\ m/s`

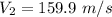
This is the outlet velocity.

Now by putting the values in equation 2

`T_2=1.81* 159.9`

`T_2=290.6K`

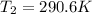
This is the outlet temperature.