Question

Eddie the Eagle, British Olympic ski jumper, is attempting his most mediocre jump yet. After leaving the end of the ski ramp, he lands downhill at a point that is displaced 64.3 m horizontally from the edge of the ramp. His velocity just before landing is 29.0 m/s and points in a direction 34.0$^\circ$ below the horizontal. Neglect any effects due to air resistance or lift.

a-What was the magnitude of Eddie's initial velocity as he left the ramp?
b-Determine Eddie's initial direction of motion as he left the ramp, measured relative to the horizontal.
c-Calculate the height of the ramp's edge relative to where Eddie landed.

Answer 1

a) The magnitude of the initial velocity was 24.0 m/s

b) The direction of motion was 0º relative to the horizontal.

c) the height of the ramp was 35.2 m

Step-by-step explanation:

Please, see the figure for a graphical description of the problem.

In a parabolic motion the equations that describe the movement are:

r = (x0 + v0 · t · cos ϴ, y0 + v0 · t · sin ϴ + 1/2 · g · t²)

v= (v0 · cos ϴ, v0 · sin ϴ + g · t)

Where:

r = position vector at time t

x0 = initial horizontal position

v0 = initial velocity

t = time

ϴ = jumping angle

y0 = initial vertical position

g = acceleration due to gravity

v = vector velocity at time t

First, let´s calculate v0x and vy (see figure) using the angle of the final velocity and its magnitude. Notice that the horizontal velocity is constant during all the trajectory and its value is v0x.

From trigonmetry of right triangles, we know that:

sin α = opposite / hypotenuse

Notice that in this case the angle we should use is indicated as α in the figure. Its value is 180-90-34 = 56º. Then:

sin 56º = v0x/ v

v· sin 56º = v0x

29.0 m/s ·sin 56º = v0x

v0x = 24.0 m/s

cos 56º = vy /v

v · cos 56º = vy

29.0 m/s · cos 56º = vy

vy = 16.2 m/s

We know that, at the final time, the x-component of the vector r, rx, is 64.3 m (see figure). Then, using the equation of the x-component of r, we can obtain how much time it takes Eddie to land:

x = x0 + v0 · t · cos ϴ

Since the origin of the reference system is located at the point of the jump, x0 = 0. Also, notice that v0 · cos ϴ = v0x. Then:

64.3 m = 24.0 m/s · t

t = 64.3 m / 24.0 m/s = 2.68 s

Knowing that at final time (2.68 s) the y-component of the vector velocity is -16.2 m/s (calculated above), we can obtain v0y (v0 · sin ϴ)

vy = v0 · sin ϴ + g · t

vy = v0y + g · t

-16.2 m/s = v0y - 9.8 m/s² · 2.68 s

v0y = 0.612 m/s

Then, the magnitude of the initial velocity will be:

`|v0| = \sqrt{(v0x)^(2) + (v0y)^(2) }`

`|v0| = \sqrt{(24.0 m/s)^(2) + (0.612 m/s)^(2)} = 24.0 m/s`

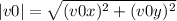
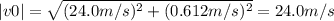
The magnitude of the initial velocity is 24.0 m/s

b)Knowing v0 and v0x, we can obtain ϴ using trigonometry:

cos ϴ = v0x/v0 = 24.0 m/s / 24.0 m/s = 1

ϴ = 0º

Eddie did not jump!

If we use the sin ϴ and v0y, we will get a similar angle.

c) To calculate the height of the ramp, we have to calculate the magnitude of the y-component of the vector "r final" in the figure, denoted as ry:

y = y0 + v0 · t · sin ϴ + 1/2 · g · t² (y0 = 0 since the point of jump is the center of our reference system)

Since sin 0º = 0:

y = -1/2 · 9.8 m/s² · (2.68 s)² = -35.7 m

The height of the ramp is 35.2 m