Answer:
If the textbook receives a favorable review, there is a 21.57% probability that it will be a huge success.
Explanation:
We have the following probabilities:
-A 10% probability that the textbook is a huge success.
-A 20% probability that the textbook is a modest success.
-A 50% probability that the textbook breaks even
-A 20% probability that the textbook is a loser
-If the book is a huge success, there is a 99% probability that it receives favorable reviews.
-If the book is a moderate success, there is a 60% probability that it receives favorable reviews.
-If the book breaks even, there is a 40% probability that it receives favorable reviews.
-If the book is a loser, there is a 20% probability that it receives favorable reviews.
If the textbook receives a favorable review, what is the probability that it will be huge success?
This can be formulated as the following problem:
What is the probability of B happening, knowing that A has happened.
It can be calculated by the following formula
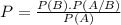
Where P(B) is the probability of B happening, P(A/B) is the probability of A happening knowing that B happened and P(A) is the probability of A happening.
So, for this problem.
What is the probability that the book is a huge success, given that it received favorable reviews?
P(B) is the probability that the book is a huge success. So:
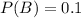
P(A/B) is the probability that the book receives favorable reviews when it is a huge success. So:
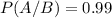
P(A) is the probability that the book receives favorable reviews:
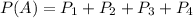
 is the probability that a book that is a huge success is chosen and receives favorable reviews. So:
is the probability that a book that is a huge success is chosen and receives favorable reviews. So:

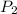 is the probability that a book that is a moderate success is chosen and receives favorable reviews. So:
is the probability that a book that is a moderate success is chosen and receives favorable reviews. So:
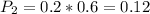
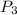 is the probability that a book that breaks even is chosen and receives favorable reviews. So:
is the probability that a book that breaks even is chosen and receives favorable reviews. So:
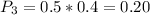
 is the probability that a book that is a loser is chosen and receives favorable reviews. So:
is the probability that a book that is a loser is chosen and receives favorable reviews. So:

So
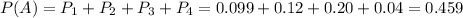
If the textbook receives a favorable review, what is the probability that it will be huge success?
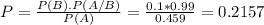
If the textbook receives a favorable review, there is a 21.57% probability that it will be a huge success.