Question

Two painters, Ray and Taylor, are painting a fence. Ray paints at a uniform rate of 40 feet every 160 minutes, and Taylor paints at a uniform rate of 50 feet every 125 minutes. Of the two painters paint simultaneously, how many minutes will it take for them to paint a fence that is 260 feet long?

Answer 1

`(40)/(160) (feet)/(minute)*x +(50)/(125) (feet)/(minute)*x = 260 feet`

`0.25(feet)/(minute)*x + 0.4(feet)/(minute)*x = 260 feet`

`x=(260)/(0.65) minutes = 400 minutes`

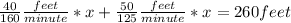
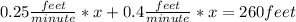
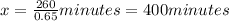
Explanation:

This problem can be solved by transforming the information into an equation.

We are looking for the number of minutes (the time) Ray and Taylor need to paint a 260 feet long fence. So let the unknown
`x` be the time in minutes.

Ray and Taylor paint with different uniforms rates. First of all we can transform these rates in speed in order to know how many feet every 1 minute they can paint.

Ray paints at a uniform rate of 40 feet every 160 minutes. So he paints with a speed of
`(40)/(160) (feet)/(minute) =(1)/(4) (feet)/(minute)=0.25(feet)/(minute)`

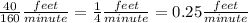
Taylor paints at a uniform rate of 50 feet every 125 minutes. So he paints with a speed of
`(50)/(125) (feet)/(minute) =(2)/(5) (feet)/(minute)=0.4(feet)/(minute)`

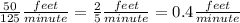
If we multiply the speed of each one by the time they will spend painting we will get the lengths each one will paint. And the sum of these lengths have to result in 260feet.

So the equation is:

`0.25(feet)/(minute)*x + 0.4(feet)/(minute)*x = 260 feet`

`(0.25+0.4)(feet)/(minute)*x = 260 feet`

`(0.65)(feet)/(minute)*x = 260 feet`

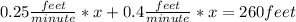
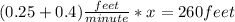
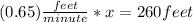
We now isolate the unknow
`x`

⇒
`x=(260)/(0.65) minutes = 400 minutes`

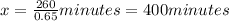
So it will take 400 minutes for Ray an Taylor to paint a fence that is 260 feet long.