Question

A scuba diver at 70 m below the surface of a lake, where the temperature is 4 degrees C, releases an air bubble with a volume of 14 cm^3. The bubble rises to the surface, where the temperature is 23 degrees C. What is the volume of the bubble (in cubic centimeters) just before it reaches the surface? (The density of water is 1000 kg/m^3 and air pressure is 1E+05 N/m^2.)

Answer 1

121.3 cm^3

Step-by-step explanation:

P1 = Po + 70 m water pressure (at a depth)

P2 = Po (at the surface)

T1 = 4°C = 273 + 4 = 277 K

V1 = 14 cm^3

T2 = 23 °C = 273 + 23 = 300 K

Let the volume of bubble at the surface of the lake is V2.

Density of water, d = 1000 kg/m^3

Po = atmospheric pressure = 10^5 N/m^2

P1 = 10^5 + 70 x 1000 x 10 = 8 x 10^5 N/m^2

Use the ideal gas equation

`(P_(1)V_(1))/(T_(1))=(P_(2)V_(2))/(T_(2))`

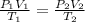
By substituting the values, we get

`(8* 10^5* 14)/(277)=(10^(5) *V_(2))/(300)`

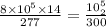
V2 = 121.3 cm^3

Thus, the volume of bubble at the surface of lake is 121.3 cm^3.