Question

Solve the triangle.

B = 36°, a = 41, c = 20

Answer 1

See below

Explanation:

When you have 2 sides and the angle between them you use the cosine theorem or law of cosines:

`b^(2)=a^(2)+c^(2)-2acCos(B)`

`b^(2)=41^(2)+20^(2)-2(41)(20)cos36 \\b^(2)=1681 + 400-1327 \\b^(2)=754 \\b = 27.5`

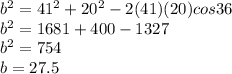
After you have a side and the opposed angle (side b and angle B), you use the law of sines:

`(a)/(sinA) =(b)/(sinB)=(c)/(sinC)`

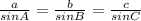
I will calculate angle A first:

`[tex](27.5)/(sin36) =(41)/(sinA) \\sinA =(41)/(27.5) sin36 \\sin A = 0.876 \\A = 61.2\°`[/tex]

Same for angle C:

`(27.5)/(sin36) =(20)/(sinC) \\sinC =(20)/(27.5) sin36 \\sin C = 0.427 \\C = 25.3\°`

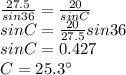
The sum of the angles is 36° + 61.2° + 25.3° = 122.5°; The sum must be 180° so this isnt a triangle.

I re did the problem using B as 63° instead of 36° in case you wrote it wrong and I got a satisfactory answer.

using B = 36:

b = 36.6

angle A = 86.4°

angle C = 29.1°

A+B+C = 86.4° + 29.1° + 63° = 178.5° ~ 180°