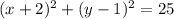Question

Which equation represents a circle that contains the point (–5, –3) and has a center at (–2, 1)? Distance formula: StartRoot (x 2 minus x 1) squared + (y 2 minus y 1) squared EndRoot

Answer 1

(x + 2)2 + (y – 1)2 = 25

Explanation:

Answer 2

The equation of the circle is
`(x+2)^2+(y-1)^2=25`

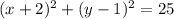
Explanation:

we know that

The equation of a circle in standard form is equal to

`(x-h)^2+(y-k)^2=r^2`

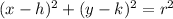
where

(h,k) is the center

r is the radius

step 1

Find the radius of the circle

The radius of the circle is equal to the distance from the center to any point on the circle

we have

(–5, –3) and (–2, 1)

Find the distance

the formula to calculate the distance between two points is equal to

`d=\sqrt{(y2-y1)^(2)+(x2-x1)^(2)}`

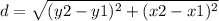
substitute

`r=\sqrt{(1+3)^(2)+(-2+5)^(2)}`

`r=\sqrt{(4)^(2)+(3)^(2)}`

`r=√(25)`

`r=5\ units`

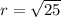
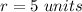
step 2

Find the equation of the circle

we have

`r=5\ units`

`(h,k)=(-2,1)`

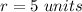
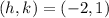
substitute

`(x-h)^2+(y-k)^2=r^2`

`(x+2)^2+(y-1)^2=5^2`

`(x+2)^2+(y-1)^2=25`

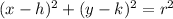
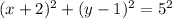
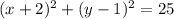
therefore

The equation of the circle is
`(x+2)^2+(y-1)^2=25`