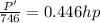Question

A fan draws air from the atmosphere through a 0.30‐m‐diameter round duct that has a smoothly rounded entrance. A differential manometer connected to an opening in the wall of the duct shows a vacuum pressure of 2.5 cm of water. The density of air is 1.22 kg/m3. Determine the volume rate of air flow in the duct in cubic feet per second. What is the horsepower output of the fan?

Answer 1

The volume air flow rate is
`47.92 ft^(3)/s`

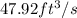
The output of the fan is 0.446 hp

Solution:

As per the question:

Diameter of the round duct, d = 0.30 m

Radius of the duct, R =
`(d)/(2) = (0.30)/(2) = 0.15 m`

Pressure of the opening, P = 2.5 cm of water = 0.025 m of water

P =
`0.025* 9.8* 1000 = 245 Pa`

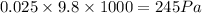
Density of air,
`\rho_(a) = 1.22 kg/m^(3)`

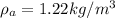
Now, the velocity, v can be calculated as:

`\Delta P = (1)/(2)\rho_(a) v^(2)`

`v = \sqrt{(2\Delta P)/(\rho_(a))`

`v = \sqrt{(2* 245)/(1.22) = 19.212 m/s`

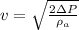
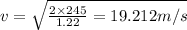
Now,

Volume rate of air flow is given by:

`V_(f) = Av = \pi R^(2)* v`

`V_(f) = Av = \pi (0.15)^(2)* 19.21 = 1.357 m^(3)/s`

Now,

1 ft = 3.2808 m

`V_(f) = 1.357* (3.2808)^(3) = 47.92  ft^(3)/s`

Now, the output of the fan in horsepower (hp):

Power output, P' =
`\Delta P* V = 245* 1.36 = 333.2 W`

Now,

1 hp = 746 W

P' (in hp) =
`(P')/(746) = 0.446 hp`