Question

Phyllis invested $11,500, a portion earning a simple interest rate of

3 1/5% per year and the rest earning a rate of 3% per year. After one year the total interest earned on these investments was $362.00. How much money did she invest at each rate?

Answer 1

He invested $8500 with rate 3 1/5%

He invested $3000 with rate 3%

Explanation:

* Lets revise the rule of the simple interest

- Simple interest I = PRT, where P in the money invested, R is the

interest rate and T is the time of investment

- Phyllis invested $11,500

- A portion earning a simple interest rate of 3 1/5% (3.2%) per year

- The rest earning a rate of 3% per year

- After one year the total interest earned on these investments

was $362.00

- We need to find the amount of money invested in each rate

* Assume that he invested $x with rate 3 1/5% and $y with rate 3%

∵ He invested $11,500 in both rates

∴ x + y = 11,500 ⇒ (1)

∵ He invested $x with 3 1/5%

∵ P = $x

∵ R = 3.2/100 = 0.032

∵ T = 1

∴
`I_(1)=x(0.032)(1)`

∴
`I_(1)=0.032x`

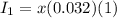
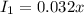
∵ He invested $y with 3%

∵ P = $y

∵ R = 3/100 = 0.03

∵ T = 1

∴
`I_(2)=y(0.03)(1)`

∴
`I_(2)=0.03y`

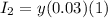
∵ The total interest was $362.00

- The total interest =
`I_(1)` +
`I_(2)`

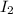
∴ 0.032x + 0.03y = 362.00 ⇒ (2)

We have system of equations

x + y = 11,500 ⇒ (1)

0.032x + 0.03y = 362.00 ⇒ (2)

Multiply equation (1) by -0.03 to eliminate y

-0.03x - 0.03y = 345 ⇒ (3)

Add equations (2) and (3)

0.002x = 17

Divide both sides by 0.002

x = 8500

Substitute the value of x in equation (1)

8500 + y = 11,500

Subtract 8500 from both sides

y = 3000

* He invested $8500 with rate 3 1/5%

* He invested $3000 with rate 3%