Question

f a solution containing 85.14 g of mercury(II) nitrate is allowed to react completely with a solution containing 14.334 g of sodium sulfide, how many grams of solid precipitate will be formed? mass: 29.69 g How many grams of the reactant in excess will remain after the reaction? mass: g Assuming complete precipitation, how many moles of each ion remain in solution? If an ion is no longer in solution, enter a zero (0) for the number of moles. Hg2+ : 0 mol NO–3 : 0 mol Na+ : 0 mol S2− : 0 mol

Answer 1

• The reaction that takes place is:

Hg(NO₃)₂(ac) + Na₂S(ac) → HgS(s) + 2Na⁺ + 2NO₃⁻

Now we calculate the moles of each reagent -using the molecular weights-, in order to determine the limiting reactant:

• Moles of mercury (II) nitrate = 85.14 g *
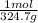  `(1mol)/(324.7g)`=0.2622 moles.
• Moles of sodium sulfide = 14.334 g *
  `(1mol)/(78.04g)`=0.1837 moles.

Because the stoichiometric ratio between the reactants is 1:1, we compare the number of moles of each one upfront.

moles Hg(NO₃)₂ > moles Na₂S

Thus Na₂S is the limiting reagent.

So in order to find the mass of solid precipitate, we must calculate it using the moles of Na₂S:

`0.1837 molNa_(2) S*(1molHgS )/(1molNa_(2)S)*(232.66g)/(1molHgS) =42.740g`

The mass of the solid precipitate is 42.760 g.

• In order to calculate the grams of the reactant in excess that will remain after the reaction, we convert the moles that reacted into mass and substract them from the original mass:

Mass of Hg(NO₃)₂ remaining =
`85.14g-(0.1837molHg(NO_(3))_(2) * 324.7 g/mol)=25.49g`

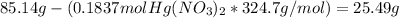
The mass of the remaning reactant in excess is 25.49 g.

• Because we assume complete precipitation, there are no more Hg⁺² or S⁻² ions in solution. The moles of NO₃⁻ and Na⁺ in solution remain the same during the reaction, so the number is calculated from the number added in the reactant:

Hg⁺²: 0 mol

NO₃⁻:
`0.2622molHg(NO_(3))_(2) *(2molNO_(3)^(-))/(1molHg(NO_(3))_(2) *) =0.5244molNO_(3)^(-)`

Na⁺:
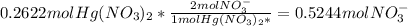
`0.1837molNa_(2) S*(1molNa^(+))/(1molNa_(2))=0.1837molNa^(+)`

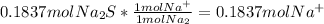
S²⁻: 0 mol