Question

A company has a budget of $280,000 for computing equipment. Tablets cost $500 each, laptops cost $2000 each, and servers cost $5000 each. The company needs 5 times as many tablets as laptops, and two times as many laptops as servers. Set this problem up as a system of three linear equations, and use trial and error to determine the approximate number of each type of machine should be purchased.

Answer 1

The number of tablets 200

the number of laptops 40

and, the number of servers 20

Explanation:

Let the number of tablets be 'x'

the number of laptops be 'y'

and, the number of servers be 'z'

According to the given question

Total budget = $280,000

Tablets cost = $500 each

laptops cost = $2000 each

servers cost = $5000 each

Thus,

500x + 2000y + 5000z = 280,000 ..............(1)

also,

x = 5y ................(2)

and,

y = 2z

or

z =
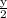`\frac{\textup{y}}{\textup{2}}` ............(3)

substituting y from 2 and 3 in equation 1, we get

(500 × 5y) + (2000 × y) + (5000 ×
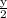`\frac{\textup{y}}{\textup{2}}` ) = 280,000

or

2500y + 2000y + 2500y = 280,000

or

7000y = 280,000

or

y = 40

substituting y in equation 2, we get

x = 5 × 40 = 200

substituting y in equation 3 we get

z =
`\frac{\textup{40}}{\textup{2}}`

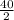
or

z = 20

hence,

the number of tablets 200

the number of laptops 40

and, the number of servers 20