Answer:
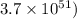 kg
kg
Step-by-step explanation:
 = radius of the sphere modeled as universe =
= radius of the sphere modeled as universe =
 m
m
Volume of sphere is given as
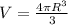
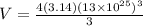
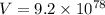 m³
m³
 = average total mass density of universe =
= average total mass density of universe =
 kg/m³
kg/m³
 = Total mass of the universe = ?
= Total mass of the universe = ?
We know that mass is the product of volume and density, hence
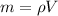
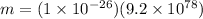
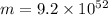 kg
kg
 = mass of "ordinary" matter = ?
= mass of "ordinary" matter = ?
mass of "ordinary" matter is only about 4% of total mass, hence

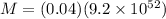
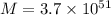 kg
kg