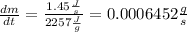Question

A cold beverage can be kept cold even a warm day if it is slipped into a porous ceramic container that has been soaked in water. Assume that energy lost to evaporation matches the net energy gained via the radiation exchange through the top and the side surfaces. The container and beverage have temperature T = 17°C, the environment has temperature Tenv = 32°C, and the container is a cylinder with radius r = 2.52 cm and height 9 cm. Approximately the emissivity as ε = 1, and neglect other energy exchanges. At what rate dm/dt is the container losing water mass?

Answer 1

The rate at which the container is losing water is 0.0006418 g/s.

Step-by-step explanation:

1. Under the assumption that the can is a closed system, the conservation law applied to the system would be:
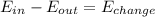   `E_(in)-E_(out)=E_(change)`, where
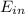   `E_(in)` is all energy entering the system,
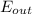   `E_(out)` is the total energy leaving the system and,
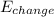   `E_(change)` is the change of energy of the system.
2. As the purpose is to kept the beverage can at constant temperature, the change of energy (
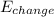   `E_(change)`) would be 0.
3. The energy that goes into the system, is the heat transfer by radiation from the environment to the top and side surfaces of the can. This kind of transfer is described by:
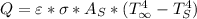   `Q=\varepsilon*\sigma*A_S*(T_(\infty)^4-T_S^4)` where
   `\varepsilon` is the emissivity of the surface,
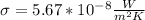   `\sigma=5.67*10^(-8)(W)/(m^2K)` known as the Stefan–Boltzmann constant,
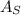   `A_S` is the total area of the exposed surface,
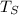   `T_S` is the temperature of the surface in Kelvin,
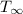   `T_(\infty)` is the environment temperature in Kelvin.
4. For the can the surface area would be ta sum of the top and the sides. The area of the top would be
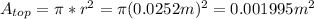   `A_(top)=\pi* r^2=\pi(0.0252m)^2=0.001995m^2`, the area of the sides would be
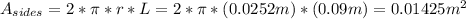   `A_(sides)=2*\pi*r*L=2*\pi*(0.0252m)*(0.09m)=0.01425m^2`. Then the total area would be
   `A_(total)=A_(top)+A_(sides)=0.01624m^2`
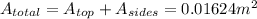
5. Then the radiation heat transferred to the can would be
   `Q=\varepsilon*\sigma*A_S*(T_(\infty)^4-T_S^4)=1*5.67*10^(-8)(W)/(m^2K)*0.01624m^2*((32+273K)^4-(17+273K)^4)=1.456W`.
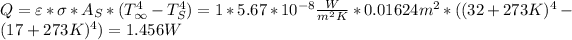6. The can would lost heat evaporating water, in this case would be
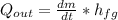   `Q_(out)=(dm)/(dt)*h_(fg)`, where
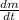   `(dm)/(dt)` is the rate of mass of water evaporated and,
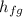   `h_(fg)` is the heat of vaporization of the water (
   `2257(J)/(g)`).
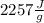7. Then in the conservation balance:
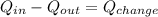   `Q_(in)-Q_(out)=Q_(change)`, it would be
   `1.45W-(dm)/(dt)*2257(j)/(g)=0`.
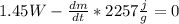8. Recall that
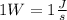   `1W=1(J)/(s)`, then solving for
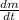   `(dm)/(dt)`:
   `(dm)/(dt)=(1.45(J)/(s) )/(2257(J)/(g) )=0.0006452(g)/(s)`