Question

The following questions present a twist on the scenario above to test your understanding. Suppose another stone is thrown horizontally from the same building. If it strikes the ground 56 m away, find the following values.

(a) time of flight 3.03 Correct: Your answer is correct. s
(b) initial speed 18.5 Correct: Your answer is correct. m/s
(c) speed and angle with respect to the horizontal of the velocity vector at impact 23.23 Incorrect: Your answer is incorrect. m/s Your response differs from the correct answer by more than 10%. Double check your calculations.

Answer 1

The first part of the text is missing, you can find on google:

"A ball is thrown horizontally from the roof of a building 45 m. If it strikes the ground 56 m away, find the following values."

Let's now solve the different parts.

(a) 3.03 s

The time of flight can be found by analyzing the vertical motion only. The vertical displacement at time t is given by

`y(t) = h -(1)/(2)gt^2`

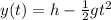
where

h = 45 m is the initial height

g = 9.8 m/s^2 is the acceleration of gravity

When y=0, the ball reaches the ground, so the time taken for this to happen can be found by substituting y=0 and solving for the time:

`0=h-(1)/(2)gt^2\\t=\sqrt{(2h)/(g)}=\sqrt{(2(45))/(9.8)}=3.03 s`

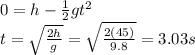
(b) 18.5 m/s

For this part, we need to analyze the horizontal motion only, which is a uniform motion at constant speed.

The horizontal position is given by

`x=v_x t`

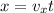
where

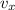`v_x` is the horizontal speed, which is constant

t is the time

At t = 3.03 s (time of flight), we know that the horizontal position is x = 56 m. By substituting these numbers and solving for vx, we find the horizontal speed:

`v_x = (x)/(t)=(56)/(3.03)=18.5 m/s`

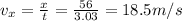
The ball was thrown horizontally: this means that its initial vertical speed was zero, so 18.5 m/s was also its initial overall speed.

(c) 35.0 m/s at 58.1 degrees below the horizontal

At the impact, we know that the horizontal speed is still the same:

`v_x = 18.5 m/s`

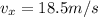
we need to find the vertical velocity. This can be done by using the equation

`v_y = u_y -gt`

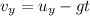
where

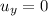`u_y =0` is the initial vertical velocity

g is the acceleration of gravity

t is the time

Substituting t = 3.03 s, we find the vertical velocity at the time of impact:

`v_y = -(9.8)(3.03)=-29.7 m/s`

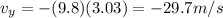
So the magnitude of the velocity at the impact (so, the speed at the impact) is

`v=√(v_x^2+v_y^2)=√(18.5^2+(-29.7)^2)=35.0 m/s`

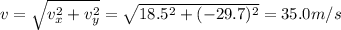
The angle instead can be found as:

`\theta=tan^(-1)((v_y)/(v_x))=tan^(-1)((-29.7)/(18.5))=-58.1^(\circ)`

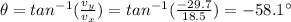
so, 58.1 degrees below the horizontal.