Question

The combination of an applied force and a friction force produces a constant total torque of 35.9 N·m on a wheel rotating about a fixed axis. The applied force acts for 6.20 s. During this time, the angular speed of the wheel increases from 0 to 9.9 rad/s. The applied force is then removed, and the wheel comes to rest in 60.7 s. a. Find the moment of inertia of the wheel. b. Find the magnitude of the torque due to friction c. Find the total number of revolutions of the wheel during the entire interval of 66.9 s.

Answer 1

Step-by-step explanation:

Given that,

Torque = 35.9 N-m

Time of acceleration= 6.20 s

Initial angular speed = 0 rad/s

Final angular speed = 9.9 rad/s

Time of declaration = 60.7 s

(a). We need to calculate the angular acceleration

Using formula of angular acceleration

`\omega_(2)=\omega_(1)+\alpha t_(1)`

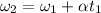
Put the value into the formula

`9.9=0+\alpha*6.2`

`\alpha=(9.9)/(6.2)`

`\alpha=1.59\ rad/s^2`

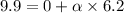
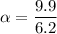
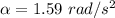
We need to calculate the moment of inertia of the wheel

Using formula of moment of inertia

`I=(\tau)/(\alpha)`

Put the value into the formula

`I=(35.9)/(1.59)`

`I=22.57\ kg-m^2`

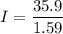
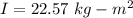
The moment of inertia of the wheel is
`22.57\ kg-m^2`

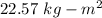
(b). The applied force is removed, then the magnitude of the torque due to friction

We need to the magnitude of the torque due to friction

Using equation of rotation

`\omega_(2)=\omega_(1)+\alpha' t_(2)`

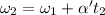
Put the value into the formula

`0=9.9+\alpha'*60.7`

`\alpha'=-(9.9)/(60.7)`

`\alpha'=-0.163\ rad/s^(2)`

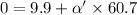
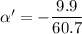
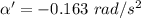
Magnitude of angular acceleration is 0.163 rad/s²

We need to calculate the frictional torque

Using formula of torque

`\tau'=I*\alpha'`

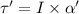
Put the value into the formula

`\tau'=22.57* 0.163`

`\tau'=3.678\ kg-m rad/s^2`

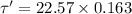
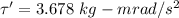
The frictional torque is
`3.678\ kg-m\ rad/s^2`

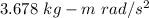
(c). We need to calculate the total number of revolutions of the wheel during the entire interval of 66.9 s

Using formula of angular displacement

During the applied force,

`\theta_(1)=(1)/(2)\alpha t_(1)^2`

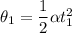
Put the value into the formula

`\theta_(1)=(1)/(2)*1.58*6.2^2`

`\theta_(1)=30.36\ rad`

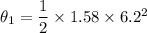
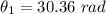
During the removed of force,

`\theta_(2)=\omega t^2+(1)/(2)\alpha' t_(2)^2`

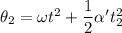
Put the value into the formula

`\theta_(2)=9.9*60.7-(1)/(2)*0.163*(60.7)^2`

`\theta_(2)=300.6\ rad`

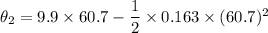
The total angular displacement

`\theta=\theta_(1)+\theta_(2)`

`\theta=30.36+300.6`

`\theta=330.96\ rad`

`\theta=(330.96)/(2\pi)`

`\theta=52.67\ rev`

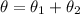
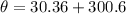
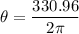
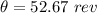
The total number of revolutions of the wheel is 52.67 rev.

Hence, This is the required solution.