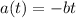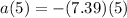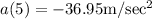Answer:
Acceleration of the particle=
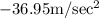
Velocity of the particle=
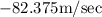
position of the particle=
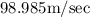
Step-by-step explanation:
Given:
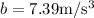
t = 0
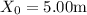
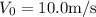
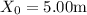
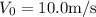
To find:
The acceleration of particle at t= 5,00 s
Velocity of the particle at t= 5,00 s
Postion of the particle at t= 5,00 s
Solution:
Finding the value of a:
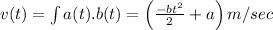
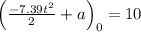
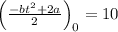
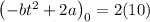
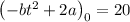
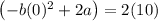
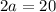
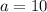
Finding the value of c
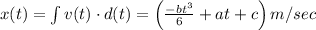
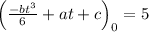
Substituting t=0
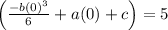
c=5
Finding the velocity of of particle at t=5
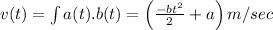
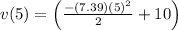
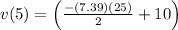
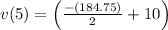
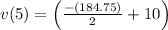
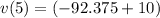
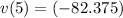
Position of the particle at x=5
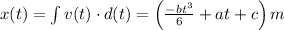
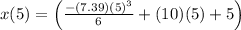
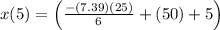
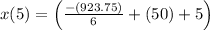
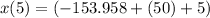
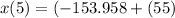
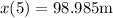
The acceleration of the particle t=5