Question

A particle of charge Q is fixed at the origin of an xy coordinate system. At t = 0 a particle (m = 0.693 g, q = 3.09 µC is located on the x axis at x = 24.6 cm, moving with a speed of 74.0 m/s in the positive y direction. For what value of Q will the moving particle execute circular motion? (Neglect the gravitational force on the particle.)

Answer 1

33.57μC

Step-by-step explanation:

The moving particle will execute a circular motion when the Electric force between the particles is equal to the centripetal force necessary for the circular motion at a velocity equal to 74m/s and a radius = 0.246m. You can find the value for the centripetal force with this expression:

`F_c = m(v^2)/(r) = 6.93*10^(-4)kg((74m/s)^2)/(0.246m) = 15.43N`

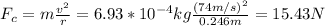
Now, this is the value that the electric force between the charges should be. The electric force is given by this expresion:

`F_e = k*(Qq)/(r^2)`

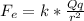
k is the Coulomb constant, equal to 9*10^9 Nm^2/C^2. Then:

`F_e = k*(Qq)/(r^2)\\Q = (F_e r^2)/(k*q) \\Q = (15.43 N*(0.246m)^2)/(9*10^9 Nm^2/C^2*3.09*10^(-6)C) = 33.57 *10^(-6)C`

Or 33.57μC