Question

Only 1% of 40-year-old women who participate in a routine mammography test have breast cancer. 80% of women who have breast cancer will test positive, but 9.6% of women who don’t have breast cancer will also get positive tests. Suppose we know that a woman of this age tested positive in a routine screening. What is the probability that she actually has breast cancer?

Answer 1

Probability that the woman has really breast cancer if the test result is positive = 0.077

Explanation:

Given,

Probability that the woman has breast cancer, P(B) = 0.01

=> Probability that the woman has breast cancer, P(B')=1-0.01= 0.99

Probability that test will be positive if woman has breast cancer,P(T/B) = 0.8

=>Probability that test will be negative if woman has breast cancer,P(T'/B) =1-0.8= 0.2

Probability that test will be positive if woman hasn't breast cancer,P(T/B')=0.096

=>Probability that test will be negative if woman hasn't breast cancer,P(T'/B')=1-0.096=0.904

So, the probability that the test will show positive result either the disease is present or not,

P{T} = P(T/B).P(B)+P(T/B').P(B')

= 0.8 x 0.01 + 0.096 x 0.99

= 0.10304

Now, the probability that the woman has really breast cancer if the test result is positive,

`P(B/T)\ =\ (P(T/B)* P(B))/(P(T))`

`=\ (0.8* 0.01)/(0.10304)`

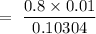
= 0.077