Question

A widget inspector inspects 12 widgets and finds that exactly 3 are defective.Unfortunately, the widgets then get all mixed up and the inspector has to find the 3defective widgets again by testing widgets one by one.(a) Find the probability that the inspector will now have to test at least 9 widgets.

Answer 1

`P[x\geq 9] = 0.0003971`

Explanation:

Given data:

n = 12

Defective widget probability is
`p = (3)/(12) = 0.25`

q = 1 - p = 0.75

Probability of test atleast 9 widget is calculated by binomial distribution as

`P[x\geq 9] = P(9) + P(10) +P(11) + P(12)`

`=\sum_(X =9)^(12) ^12C_x p^x q^(12-x)`

`= \sum_(X =9)^(12) ^12C_x (0.25)^x (0.75)^(12-x)`

`= \sum_(X =9)^(12) ^(12)C_9 (0.25)^9 (0.75)^(3) +\sum{x=9}{12} ^(12)C_(10) (0.25)^(10) (0.75)^(2) + \sum{x=9}{12} ^(12)C_(11) (0.25)^(11) (0.75)^(1)  +\sum{x=9}{12} ^(12)C_(12) (0.25)^(12) (0.75)^(0)`

= 0.003541 + 0.000354+ 0.0000021 + 0.0000001

= 0.0003971

`P[x\geq 9] = 0.0003971`

Answer 2

0.7455

Explanation:

First, we note that there are C
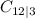`C_(12|3)` = 220 ways of selecting the defective items.

The probability that the inspector will have to test at least 9 widgets would be 1 minus the probability that the inspector will have to test 8 or less widgets.

This is 1 - P(8 or less widgets have to be checked)

1 -
`(C_(8|3) )/(C_(12|3) )`

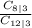
= 1 - 56/220

= 1 - 0.2545

= 0.7455