Question

The phosphate buffer system is very important for maintaining the pH of the cytoplasm of all cells. Phosphoric acid is a triprotic acid; however, the relevant equilibrium in the biologically useful, neutral range, with a pKa of 6.86, is that of dihydrogen phosphate and monohydrogen phosphate ions: H3PO4 ⇌ H2PO4- + H+ pKa = 2.14 H2PO4- ⇌ HPO42- + H+ pKa = 6.86 HPO42- ⇌ PO43- + H+ pKa = 12.4 Using the Henderson-Hasselbalch equation, calculate the pH of a solution containing 0.042 M NaH2PO4 and 0.058 M Na2HPO4.

Answer 1

The pH is 7.0

Step-by-step explanation:

The equilibrium relevant for the problem is:

H₂PO4⁻ ⇌ HPO4⁻² + H⁺ pKa = 6.86

The Henderson-Hasselbalch (H-H) equation describes the pH of a buffer solution, using the concentrations of the acid and its conjugate base:

`pH=pka+log([A^(-) ])/([HA])`

For this case, [A⁻] = [HPO4⁻²], and [HA] = [H₂PO4⁻]. Thus:

`pH=pka+log([HPO4^(-2) ])/([H2PO4^(-) ])`

We put the concentrations and pka given in the problem in the H-H equation:

`pH=6.86+log(0.058M)/(0.042M)\\pH=6.86+log(1.381)\\pH=7.0`

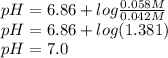
P.S.: The actual pka for the equilibrium is 7.21, according to literature. Not 6.86 like the problem says. If we use a pka of 7.21 then the pH would be 7.35.