Question

A jogger travels a route that has two parts. The first is a displacement of 2.75 km due south, and the second involves a displacement that points due east. The resultant displacement + has a magnitude of 4.60 km. (a) What is the magnitude of , and (b) what is the direction of + as a positive angle relative to due south? Suppose that - had a magnitude of 4.60 km. (c) What then would be the magnitude of , and (d) what is the direction of - relative to due south? (a) Number Units (b) Number Units

Answer 1

a) 3.7 km

b) 37°

c) 5.4 km

d) 31°

Step-by-step explanation:

The total displacement can be written as

R = (x * i + 2.75 * j) km

The magnitude of the displacement is found with Pythagoras theorem.

R^2 = x^2 + y^2

In this case we know the magnitude of the displacement and want to know x.

x^2 = R^2 - y^2

`x = √(R^2 - y^2)`

`x = √(4.6^2 - 2.75^2) = 3.7 km`

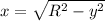
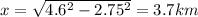
The jogger traveled 3.7 km east.

The direction of the total displacement forms an angle with the direction due south.

tg(a) = Δy/Δx

a = arctg(Δy/Δx)

a = arctg(2.75/3.7) = 37°

If I suppose the displacement to the east had a magnitude of 4.6 km, the total displacement would be of

`R = √(x^2 + y^2)`

`R = √(4.6^2 + 2.75^2) = 5.4 km`

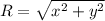
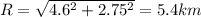
a = arctg(2.75/4.6) = 31°