Answer:
2.1
Explanation:
We know that for a discrete random variable X, the expected value of X is given by E(X) =
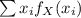 , where the values
, where the values
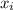 are the different values that can be taked by X, and
are the different values that can be taked by X, and
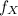 is the probability mass function of X. In other words, if the discrete random variable X can take n different values
is the probability mass function of X. In other words, if the discrete random variable X can take n different values
 with probabilities
with probabilities
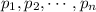 respectively, then, the expected value of X is given by E(X) =
respectively, then, the expected value of X is given by E(X) =

So, in this case we have that the expected number of times that Sam visits the gym per week in the long run is given by
E(X) = (0)(0.1) + (1)(0.15) + (2)(0.4) + (3)(0.25) + (4)(0.1) = 2.1