Question

I am stuck in Austin with a flat tire, and I need to get to my class in Houston within 2 hours. The drive is 180 miles long, but I want to be careful of the Austin cops. I do not usually get caught speeding unless I am seen accelerating too fast, so I do not want to accelerate at a rate of more than 120 mi / h2. Just to be careful, I′m going to take exactly 2 hours to make the trip. Assuming I accelerate at 120 mi / h2 for a while, and travel at a constant speed afterwards, what’s the fastest speed I′ll be going during my trip?

Answer 1

120 mi/h

Step-by-step explanation:

Given:

• 
  `u` = initial speed from where you start = 0 mi/h

• 
  `a` = acceleration for your drive =
  `120\ mi/h^2`

• 
  `s` = total distance between Austin and Houston = 180 mi

• 
  `T` = total time remaining for the journey = 2 h

Assume:

• 
  `t` = time for which you drive with constant acceleration

• 
  `r` = the remaining time for which you drive for the rest distance =
  `T-t = 2-t`

• 
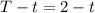
  `v` = maximum speed reached by you in the entire journey

When you start from rest and accelerate with constant acceleration for time t, you reaches your maximum speed at the last instant time of this interval. Let us first find out this speed.

`v = u+at\\\Rightarrow v = 0+at\\\Rightarrow v = at.........(1)\\`

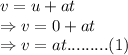
After you reach your maximum speed, you travel for the rest of the journey with this much speed. This means the sum of distances traveled during the constant acceleration and the constant speed is equal to the total distance between Austin and Houston.

`\therefore \textrm{Distance traveled during constant acceleration}+\textrm{Distance during constant speed}= \textrm{Distnace between Austin and Houston}\\`

`\Rightarrow (ut+(1)/(2)at^2)+(vr)=s\\\Rightarrow (0* t+(1)/(2)at^2)+(at)(2-t)=180\\\Rightarrow (1)/(2)at^2+2at-at^2=180\\\Rightarrow 2at-(1)/(2)at^2=180\\\Rightarrow 2* 120* t-(1)/(2)* 120* t^2=180\\\Rightarrow 240t-60t^2=180\\\Rightarrow 4t-t^2=3\\\Rightarrow t^2-4t+3\\\Rightarrow (t-1)(t-3)=0\\\Rightarrow t = 1\,\,\, or\,\,\, t = 3\\`

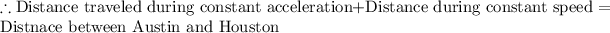
But t = 3 h is greater than the maximum allowed time.

So, t = 1 h is correct.

This means the drive must have a constant acceleration of
`120\ mi/h^2` for 1 h.

Now, on putting the value of time in equation (1), we have

`v=120* 1\\\Rightarrow v = 120\ mi/h`

Hence, the speed you will be going during the trip is 120 mi/h.