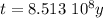Answer:
The age of the rock is
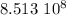 years
years
Step-by-step explanation:
We can write the formula for the quantity of material in an exponential decay as:
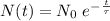
where
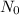 is the initial quantity of the material, and
is the initial quantity of the material, and
 is the mean lifetime of the material.
is the mean lifetime of the material.
This means that the total material that has decayed is:
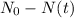
The mean lifetime can be obtained from the half-life (
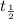 ) by the relationship
) by the relationship
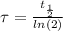
For our problem, as there was no Sr-87 present in the rock initially, and its a product of the decay, its abundance will be given by
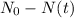 , this means, the total quantity of material that has decayed.
, this means, the total quantity of material that has decayed.
So, our equation for the ratio will be
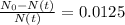

Working it a little
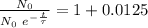
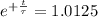
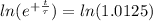


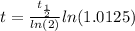
The half-life of the problem is
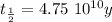
So, the age of the rock will be