Question

In the Fall STA 2023 Beginning of the Semester Survey, students were asked how many parties they attended every week and how many text messages they sent per day. The researcher decided to make the number of parties attended per week the explanatory variable and the number of text messages sent per day the response variable. The least squares regression line for this relationship is y-hat = 64.96 + 25.41x. One student attended 2 parties that week and sent 20 text messages per day. What is the residual?

Answer 1

The residual is the difference between the actual and predicted values of the response variable. In this case, the residual is 95.78 text messages.

Step-by-step explanation:

The residual represents the difference between the actual value of the response variable and the predicted value of the response variable based on the regression line. To calculate the residual, we need to substitute the given values of x (2 parties) and y (20 text messages per day) into the regression equation and find the difference between the predicted y-value (y-hat) and the actual y-value.

Using the equation y-hat = 64.96 + 25.41x, we substitute x = 2:

y-hat = 64.96 + 25.41(2) = 64.96 + 50.82 = 115.78

Therefore, the residual is the difference between the actual y-value (20) and the predicted y-value (115.78):

Residual = |20 - 115.78| = |(-95.78)| = 95.78 text messages

Answer 2

-95.78

Step-by-step explanation:

As the researcher decided to make the number of parties attended per week the explanatory variable, this would be variable x in the regression line, and of course, the variable y would be the number of text messages sent per day.

After constructing the linear regression equation, the researcher found that an approximate value
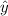`\hat y` for the actual value of y could be represented by the line

`\hat y=64.96+25.41x`

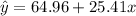
Since this is an approximate value, it is not expected that it coincides with the actual value of y. We define then the residual for each value of x as the difference between the actual value of y and the approximation for the given x.

For the value x = 2 (the student attended 2 parties that week) the actual value of y is 20 (the student sent 20 text messages per day that week).

The approximate value of y would be according to the regression line

`\hat y(2)=64.96+25.41(2)=64.96+50.82=115.78`

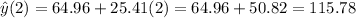
Hence, the residual value for x=2 would be

`y_(real)-\hat y=20-115.78=-95.78`