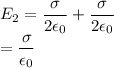Question

Two large, parallel, nonconducting sheets of positive charge face each other. What is at points (a) to the left of the sheets, (b) between them, and (c) to the right of the sheets? Assume the same surface charge density for each sheet. The separation of the sheets is much less than their dimensions. Do not consider points near the edges of the sheets. (Hint: at any point is the vector sum of the separate electric fields set up by each sheet.)

Answer 1

a)The electric Field will be zero at the point between the sheets

b)
`E_1=(\sigma)/(\epsilon_0)`

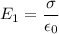
c)
`E_2=(\sigma)/(\epsilon_0)`

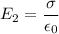
Step-by-step explanation:

Let
`\sigma` be the surface charge density of the of the non conducting parallel sheet.Let consider a Gaussian surface in the form of of cylinder such that its cross-sectional is A . Then there will be flux only due to cross sectional area as the curved sectional is perpendicular to the the electric field so the Electric Flux due to it is zero.

Now using Gauss law we have, E be the electric Field at the distance r from the sheet then

`E* 2A=(\sigma A)/(\epsilon_0)\\E=(\sigma)/(2\epsilon_0)`

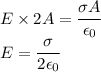
The Field will be away from the sheet and perpendicular to it.

a) The Electric Field between them

`E_1=(\sigma)/(2\epsilon_0)-(\sigma)/(2\epsilon_0)\\=0`

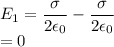
b)The Electric Field to the right of the sheets

`E_1=(\sigma)/(2\epsilon_0)+(\sigma)/(2\epsilon_0)\\=(\sigma)/(\epsilon_0)`

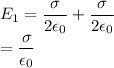
c)The Electric Field to the left of the sheets

`E_2=(\sigma)/(2\epsilon_0)+(\sigma)/(2\epsilon_0)\\=(\sigma)/(\epsilon_0)`