Question

A hot air balloon has just lifted off and is rising at the constant rate of 1.20 m/s. Suddenly, one of the passengers realizes she has left her camera on the ground. A friend picks it up and tosses it straight upward with an initial speed of 10.5 m/s. If the passenger is 3.00 m above her friend when the camera is tossed, how much time does it take for the camera to reach her?

Answer 1

Step-by-step explanation:

Speed of balloon, u = 1.2 m/s

Initial distance between balloon and camera, d = 3 m

initial speed of camera, u' = 10.5 m/s

Let the camera reaches the balloon in time t.

The distance traveled by the balloon in time t = velocity of balloon x t = 1.2 t

So, the distance traveled by the camera in time t = 3 + 1.2 t ..... (1)

By using the second equation of motion

`s=u't + 0.5 at^(2)`

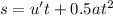
here, s s the distance traveled by the camera, u' be the initial speed of the camera, a be the acceleration due to gravity. By substituting the values, we get

`3+1.2t=10.5t - 0.5 * 9.8t^(2)`

`4.9t^(2)-9.3t+3=0`

`t=\frac{9.3\pm \sqrt{9.3^(2)-4* 4.9* 3}}{9.8}`

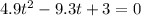
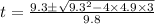
t = 0.4 s or 1.49 second