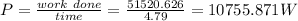Question

A(n) 591 kg elevator starts from rest. It moves upward for 4.79 s with a constant acceleration until it reaches its cruising speed of 2.17 m/s. The acceleration of gravity is 9.8 m/s 2 . Find the average power delivered by the elevator motor during the period of this acceleration. Answer in units of kW

Answer 1

Power delivered will be 10755.87 W

Step-by-step explanation:

We have given mass of elevator m = 591 kg

Time t = 4.79 sec

As the elevator starts from rest so initial velocity u = 0m/sec

Final velocity v = 2.17 m/sec

From first equation of motion

v=u+at. here v is final velocity, u is initial velocity and t is time

So
`2.17=0+a* 4.79`

`a=0.453m/sec^2`

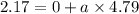
Height is given by
`h=ut+(1)/(2)at^2=0* 4.79+(1)/(2)* 0.453* 4.79^2=5.196m`

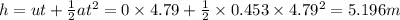
As elevator moves upward and acceleration due to gravity is downward so net acceleration due to gravity is downward so net acceleration = g-a=9.8-0.453 = 9.347
`m/sec^2`

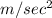
Now work done
`W=m(g-a)h=951* (9.8-0.453)* 5.196=51520.626J`

We know that power
`P=(work\ done)/(time)=(51520.626)/(4.79)=10755.871W`