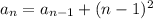Question

A playground is being designed where children can interact with their friends in certain combinations. If there is 1 child, there can be 0 interactions. If there are 2 children, there can be only 1 interaction. If there are 3 children, there can be 5 interactions. If there are 4 children, there can be 14 interactions. Which recursive equation represents the pattern?

Answer 1

Recursive equation for the pattern followed is given by,

`a_(n)=a_(n-1)+(n-1)^(2)`

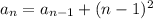
Explanation:

In the question,

The number of interaction for 1 child = 0

Number of interactions for 2 children = 1

Number of interactions for 3 children = 5

Number of interaction for 4 children = 14

So,

We need to find out the pattern for the recursive equation for the given conditions.

So,

We see that,

`a_(1)=0\\a_(2)=1\\a_(3)=5\\a_(4)=14\\`

Therefore, on checking, we observe that,

`a_(n)=a_(n-1)+(n-1)^(2)`

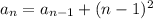
On checking the equation at the given values of 'n' of, 1, 2, 3 and 4.

At,

n = 1

`a_(n)=a_(n-1)+(n-1)^(2)\\a_(1)=a_(1-1)+(1-1)^(2)\\a_(1)=0+0=0\\a_(1)=0`

which is true.

At,

n = 2

`a_(n)=a_(n-1)+(n-1)^(2)\\a_(2)=a_(2-1)+(2-1)^(2)\\a_(2)=a_(1)+1\\a_(2)=1`

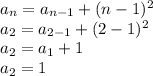
Which is also true.

At,

n = 3

`a_(n)=a_(n-1)+(n-1)^(2)\\a_(3)=a_(3-1)+(3-1)^(2)\\a_(3)=a_(2)+4\\a_(3)=5`

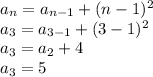
Which is true.

At,

n = 4

`a_(n)=a_(n-1)+(n-1)^(2)\\a_(4)=a_(4-1)+(4-1)^(2)\\a_(4)=a_(3)+9\\a_(4)=14`

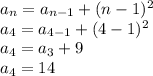
This is also true at the given value of 'n'.

Therefore, the recursive equation for the pattern followed is given by,

`a_(n)=a_(n-1)+(n-1)^(2)`