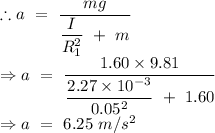Answer:
part (a)
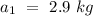
Part (b)

Step-by-step explanation:
Given,
- mass of the smaller disk =
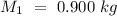
- Radius of the smaller disk =
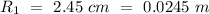
- mass of the larger disk =
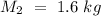
- Radius of the larger disk =
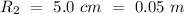
- mass of the hanging block = m = 1.60 kg
Let I be the moment of inertia of the both disk after the welding,
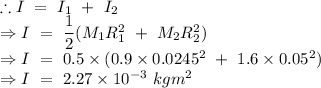
part (a)
A block of mass m is hanging on the smaller disk,
From the f.b.d. of the block,
Let 'a' be the acceleration of the block and 'T' be the tension in the string.
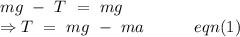
Net torque on the smaller disk,
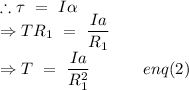
From eqn (1) and (2), we get,

part (b)
In this case the mass is rapped on the larger disk,
From the above expression of the acceleration of the block, acceleration is only depended on the radius of the rotating disk,
Let '
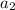 ' be the acceleration of the block in the second case,
' be the acceleration of the block in the second case,
From the above expression,