Question

A 10-year U.S. Treasury bond with a face value of $1,000 pays a coupon of 5.5% (2.75% of face value every six months). The reported yield to maturity is 5.2% (a six-month discount rate of 5.2/2 = 2.6%). What is the present value of the bond? If the yield to maturity changes to 1%, what will be the present value? If the yield to maturity changes to 8%, what will be the present value? If the yield to maturity changes to 15%, what will be the present value?

Answer 1

YTM 5.2% present value: $1,023.1644

YTM 1% present value: $1,427.2169

YTM 8% present value: $830.1209

YTM 8% present value: $515.7617

Step-by-step explanation:

YTM we will calculate the present value of the coupon payment

andthe maturity at each YTM rate given:

The coupon payment present value will be the present value of an ordinary annuity

`C * (1-(1+r)^(-time) )/(rate) = PV\\`

Coupon payment 28 (1,000 x 2.75%)

time 20 (10 years x 2 payment per year)

rate 0.026 (YTM over 2 as the payment are semiannually)

`27.5 * (1-(1+0.026)^(-20) )/(0.026) = PV\\`

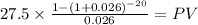
PV $424.6800

The present value of the maturity will be the present value of a lump sum:

`(Maturity)/((1 + rate)^(time) ) = PV`

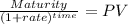
Maturity 1,000.00

time 20.00

rate 0.026

`(1000)/((1 + 0.026)^(20) ) = PV`

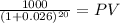
PV 598.48

PV c $424.6800

PV m $598.4843

Total $1,023.1644

Now, we will calculate changin the YTM the concept and formulas are the same, just the rate is diffrent:

If YTM = 1%

`27.5 * (1-(1+0.005)^(-20) )/(0.005) = PV\\`

`(1000)/((1 + 0.005)^(20) ) = PV`

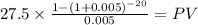
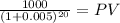
PV c $522.1540

PV m $905.0629

Total $1,427.2169

If YTM = 8%

`27.5 * (1-(1+0.04)^(-20) )/(0.04) = PV\\`

`(1000)/((1 + 0.04)^(20) ) = PV`

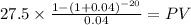
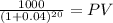
PV c $373.7340

PV m $456.3869

Total $830.1209

If YTM = 15%

`27.5 * (1-(1+0.075)^(-20) )/(0.075) = PV\\`

`(1000)/((1 + 0.075)^(20) ) = PV`

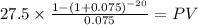
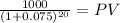
PV c $280.3485

PV m $235.4131

Total $515.7617