Question

I draw 5 cards from a deck (replacing each card immediately after it is drawn). I receive $4 for each heart that is drawn. Find the mean and variance of my total payoff

Answer 1

Each time you draw one card from the deck, there is a 13/52 = 1/4 probability of drawing a heart. If
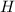`H` is a random variable representing the number of hearts you draw, then

`P(H=h)=\begin{cases}\binom5h\left(\frac14\right)^h\left(\frac34\right)^(5-h)&\text{for }0\le h\le5\\0&\text{otherwise}\end{cases}`

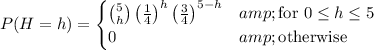
That is, the number of hearts you draw follows a binomial distribution across
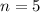`n=5` trials and with success probability
`p=\frac14`.

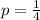You earn $4 for each heart that gets drawn; let
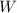`W` be the random variable denoting your total winnings. Then
`W=4H`.

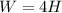Now,

`E[W]=4E[H]=4np=5`

and

`\mathrm{Var}[W]=16\mathrm{Var}[H]=16np(1-p)=15`