Answer:
a) Q1=Q2=480μC V1=240V V2=60V
b) Q1=96μC Q2=384μC V1=V2=48V
c) Q1=Q2=0C V1=V2=0V
Step-by-step explanation:
Let C1 = 2μC and C2=8μC
For part (a) of this problem, we know that charge in a series circuit, is the same in C1 and C2. Having this in mind, we can calculate equivalent capacitance first:
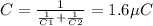

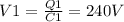
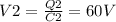
For part (b), the capacitors are in parallel now. In this condition, the voltage is the same for both capacitors:
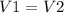 So,
So,
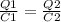
Total charge is the same calculated for part (a), so:
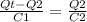 Solving for Q2:
Solving for Q2:
Q2 = 384μC Q1 = 96μC.
Therefore:
V1=V2=48V
For part (c), both capacitors would discharge, since their total voltage of 300V would by applied to a wire (R=0Ω). There would flow a huge amount of current for a short period of time, and capacitors would be completely discharged. Q1=Q2=0C V1=V2=0V