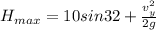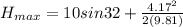Question

One side of the roof of a building slopes up at 32.0°. A roofer kicks a round, flat rock that has been thrown onto the roof by a neighborhood child. The rock slides straight up the incline with an initial speed of 15.0 m/s. The coefficient of kinetic friction between the rock and the roof is 0.355. The rock slides 10.0 m up the roof to its peak. It crosses the ridge and goes into free fall, following a parabolic trajectory above the far side of the roof, with negligible air resistance. Determine the maximum height the rock reaches above the point where it was kicked.

Answer 1

`H_(max) = 6.19 m`

Step-by-step explanation:

When rock is moving up along the inclined plane then the deceleration of the rock is given as

`a = -((\mu mg cos\theta + mgsin\theta))/(m)`

`a = -(\mu g cos\theta + g sin\theta)`

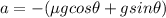
now we have

`a = -(0.355(9.81)cos32 + 9.81 sin32)`

`a = -8.15 m/s^2`

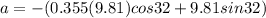
so final speed at the top of the ramp is given as

`v_f^2 - v_i^2 = 2ad`

`v_f^2 - 15^2 = 2(-8.15)(10)`

`v_f = 7.87 m/s`

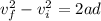
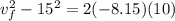
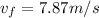
now at this point the vertical component of the velocity is given as

`v_y = v_fsin32`

`v_y = 7.87 sin32`

`v_y = 4.17 m/s`

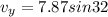
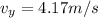
Now maximum height from the ground is given as

`H_(max) = 10sin32 + (v_y^2)/(2g)`

`H_(max) = 10sin32 + (4.17^2)/(2(9.81))`

`H_(max) = 6.19 m`