Question

A bee wants to fly to a flower located due North of the hive on a windy day. The wind blows from East to West at speed 2.79 m/s. The airspeed of the bee (i.e., its speed relative to the air) is 8.75 m/s. In which direction should the bee head in order to fly directly to the flower, due North relative to the ground? Answer in units of ◦ East of North.

Answer 1

The bee should aim at an angle of 17.69° east of north to compensate for the east to west wind, ensuring it reaches the flower directly to the north.

Step-by-step explanation:

To find the direction in which the bee should head to reach the flower directly north while compensating for the east-to-west wind, we must use vector addition. The airspeed of the bee is 8.75 m/s and it must be combined with the wind speed of 2.79 m/s blowing from east to west. The bee must aim slightly east of north to counteract the wind's influence.

Using the Pythagorean theorem and trigonometric functions, we calculate the angle θ at which the bee must fly relative to the north. To do so, we set up a right triangle where the wind speed is the opposite side, and the bee's airspeed is the hypotenuse. Using the inverse tangent function, we find θ = arctan(wind speed / airspeed). Substituting the given values, we get θ = arctan(2.79 / 8.75), which calculates to approx. 17.69°.

Therefore, the bee must fly at an angle of 17.69° east of north to reach the flower directly north. *

*These calculations assume no other forces are acting on the bee and that the wind and airspeed are constant.

Answer 2

The bee should fly 17.7º east of north.

Step-by-step explanation:

Please, see the figure for a description of the problem.

Assuming the hive as the center of our reference system

The vector velocity of the bee is:

v bee = (0, 8.75)

The vector velocity of the wind is:

v wind = (-2.79, 0)

Without course correction, the resulting vector velocity of the bee would be:

v bee + v wind = (0, 8.75) + (-2.79, 0) = (0-2.79, 8.75 + 0) = (-2.79, 8.75)

to anulate the effect of the wind, the bee should move with a velocty vector: v corrected = (2.79, 8.75) (see figure).

Now, the sum of the vector velocity of the wind and v correctd will give this resulting vector:

v wind + v corrected = (-2.79, 0) + (2.79, 8.75) = (0, 8.75) which is the original vector of the bee heading north.

Using trigonometry we can obtain the angle θ. (see figure)

sin θ = opposite / hypotenuse

then:

sin θ = magnitude of v wind / magnitude of v corrected

or

cos θ = adjacent / hypotenuse

cos θ = magnitude of v bee / magnitude of v corrected

magnitude of v wind =
`|v wind| = \sqrt{(-2.79)^(2)+0^(2)} = 2.79`

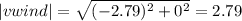
magnitude of v corrected =
`|v corrected| = \sqrt{(2.79)^(2) + (8.75)^(2)}= 9.18`

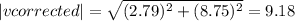
Then:

sin θ = 2.79 / 9.18

θ = 17.7º

The bee should fly 17.7º east of north.