Answer: 0.0386
Explanation:
Given: The probability hat the frozen chickens contain enough salmonella bacteria to cause illness if improperly cooked : p= 0.30
Sample size : n = 12
Let x = Number of contaminated chickens
Here , two outcomes for any chicken (either contaminated or not) , so it follows binomial distribution.
Binomial probability formula:
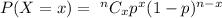
The probability that the consumer will have more than 6 contaminated chickens :-
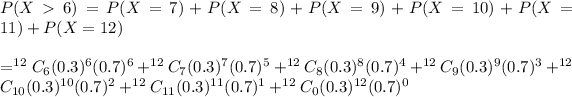
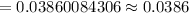 (simplified)
(simplified)
Hence, the required probability = 0.0386