Answer : The correct rate law for the reaction is,
![\text{Rate}=k[CHCl_3][Cl_2]^(1/2)](https://img.qammunity.org/2020/formulas/chemistry/college/l1bjl3428g1sgf351eali4r4xtlb89545t.png)
Explanation :
Rate law : It is defined as the expression which expresses the rate of the reaction in terms of molar concentration of the reactants with each term raised to the power their stoichiometric coefficient of that reactant in the balanced chemical equation.
For the given chemical equation:
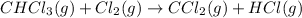
Rate law expression for the reaction:
![\text{Rate}=k[CHCl_3]^a[Cl_2]^b](https://img.qammunity.org/2020/formulas/chemistry/college/205tj6q44rkr6gir558hnpmtsyrtaamubu.png)
where,
a = order with respect to
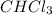
b = order with respect to
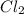
Expression for rate law for first observation:
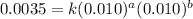 ....(1)
....(1)
Expression for rate law for second observation:
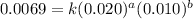 ....(2)
....(2)
Expression for rate law for third observation:
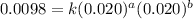 ....(3)
....(3)
Expression for rate law for fourth observation:
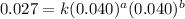 ....(4)
....(4)
Dividing 1 from 2, we get:
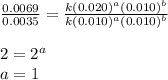
Dividing 2 from 3, we get:
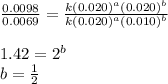
Calculation used :
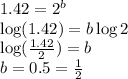
Thus, the rate law becomes:
![\text{Rate}=k[CHCl_3]^1[Cl_2]^(1/2)](https://img.qammunity.org/2020/formulas/chemistry/college/4sf9jzunqf433kpx0q0vno9cex03izlxbp.png)