Question

Assume a and b are nonzero rational numbers and c is an irrational number. For each of the following expressions, determine whether the result is irrational, rational, or both. Justify your answers. Part A: a(b + c) (1 point) Part B: (1 point) Part C: ab + ab2 (2 points)

Answer 1

Irrational Number...............

Rational Number.......................

Answer 2

A.Irrational number

C.Rational number

Explanation:

We are given that a and b are non zero rational number and c is an irrational number .

A.We have to find a(b+c) is rational, irrational or both.

a=Rational number

b=Rational number

c=Irrational number

We know that sum of a rational number and an irrational number=Irrational number.

Therefore, b+c=Irrational number

When an irrational number multiplied by a rational number then it is an irrational number.

Suppose , a=1 and b=5

c=
`\sqrt3`

`b+c=2+\sqrt3`

`a\cdot(b+c)=1\cdot (2+\sqrt3)=2+\sqrt3`

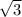
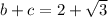
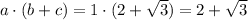
Hence, a(b+c) is an irrational number.

C.We
`ab+ab^2`

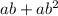
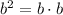`b^2=b\cdot b`=Rational number

ab=Rational number.
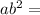`ab^2=`Rational number

Product of two rational number is also rational number .

Sum of two rational numbers is also rational number.

Hence,
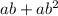`ab+ab^2` is a rational number.