Question

A rectangular piece of land whose length is twice its width has a diagonal distance of 90 yards. How many​ yards, to the nearest tenth of a​ yard, does a person save by walking diagonally across the land instead of walking its length and its​ width?

Answer 1

A person saves 30.7 yards

Explanation:

the path a person walks diagonally creates a right triangle with the lenght and the width of the rectangular piece of land. The diagonal is 90 yards which becomes the hypotenuse.

let w be the width, then l becomes the length, which is twice the width. Therefore, leg l=2a and leg w=a.

By the Pythagorean Theorem:

`c^(2)=l^(2)+w^(2)`

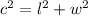
Replacing the values:

`90^(2)=(2a)^(2)+a^(2)\\90^(2)=4a^(2)+a^(2)\\90^(2)=5a^(2)\\\\a=\sqrt{(90^(2))/(5) } } =(90)/(√(5) )`

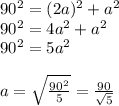
But that a is the value for the width, if a person walks the width and the length, it becomes:

the length plus the width=2a+a=3a.

So:

`a=(90)/(√(5) ) \\\\3a=(3(90))/(√(5) )`

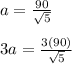
Now, the difference between walking across the land and surrounding it, is:

`d=(3(90))/(√(5) )-90=30.7476\\\\d=30.7`

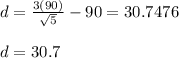
We can conclude, a person saves 30.7 yards if walking across the land.