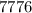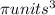2 Answers

Tatjana Heuser · Answer 1 · 2020-08-25T09:35:59+0000

Answer:

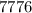
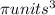
$\pi units^(3)$

Step-by-step explanation: To find the volume of a sphere, start with the formula for the volume of sphere.

Volume =
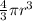
$(4)/(3) \pi r^(3)$

Notice that our sphere has a radius of 18 units, so we can plug 18 into the formula.

Volume =
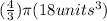
$((4)/(3)\))\pi(18units^(3))$

Now, let's start by simplifying the exponent.
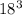18^(3) is equal to 18 units x 18 units x 18 units or 5,832 units³.

Volume =
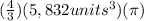
$((4)/(3)) (5,832 units^(3)) (\pi)$

Notice that we can cross cancel 3 in
(4)/(3) and 5,832 to 1 and 1,944.

Volume =
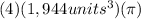
$(4) (1,944 units^(3))(\pi)$

Volume =
7776
$\pi units^(3)$

Please log in or register to add a comment.