Answer:
(a):
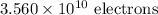
(b):
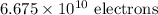
Step-by-step explanation:
Given:
- Length of the rod, L = 3.06 m.
- Cross-sectional area of the rod, A = 4.32 cm² =
 .
.
The charge on a single electron,
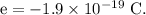
The excess number of electrons on the rod is equal to the net charge on the rod divided by the charge on a single electron.
(a): If the volume charge density of the rod is uniform.
Uniform volume charge density of the rod,
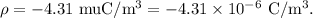
For the uniform charge density, the total charge on the rod is equal to the product of volume of the rod and the volume charge density of the rod.
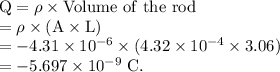
If there are n number of excess electron on the rod, then,
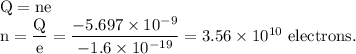
(b): If the volume charge density of the rod is non-uniform.
Non-uniform volume charge density of the rod,
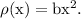
where,
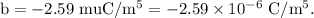
For the non-uniform charge density of the rod, the total charge on the rod is given by
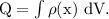
where, dV is the volume element of the rod whose length is dx, therefore, dV = A dx.
The rod is extended from origin to length L, therefore, the total charge on the rod is given by,
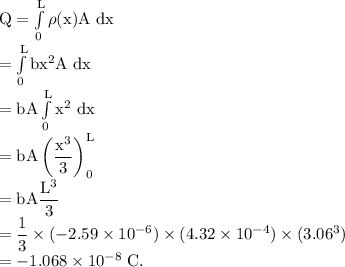
If there are n number of excess electron on the rod, then,
