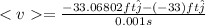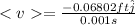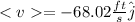A ball is thrown into the air by a baby alien on a planet in the system of Alpha Centauri with a velocity of 46 ft/s. Its height in feet after t seconds is given by y=46t−19t2. …

A ball is thrown into the air by a baby alien on a planet in the system of Alpha Centauri with a velocity of 46 ft/s. Its height in feet after t seconds is given by y=46t−19t2. …

asked Jun 25, 2020 116k views

1 Answer

Answer:

The average velocities are:

for 0.01.s

$<v> = - 68.19 (ft)/(s) \hat{j}$

for 0.005 s

$<v> = - 68.2 (ft)/(s) \hat{j}$

for 0.002 s

$<v> = - 68.05 (ft)/(s) \hat{j}$

for 0.001 s

$<v> = - 68.02 (ft)/(s) \hat{j}$

Step-by-step explanation:

The average velocity is given by

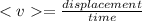
<v> = (displacement)/(time)

So, we just need to find the position at t = 3 s and then, after every period of time.

Position at t = 3 s

Knowing that

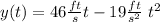
$y(t) = 46 (ft)/(s) t - 19 (ft)/(s^2) \ t^2$

at t = 3 s we have

$y(3 \ s) = 46 (ft)/(s) * 3 s - 19 (ft)/(s^2) * (3 \ s)^2$

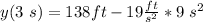
$y(3 \ s) = 138 ft - 19(ft)/(s^2) * 9 \ s^2$

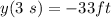
$y(3 \ s) = -33 ft$

After 0.01 s

After 0.01 s the position will be

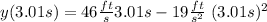
$y(3.01 s) = 46 (ft)/(s) 3.01 s - 19 (ft)/(s^2) \ (3.01 s)^2$

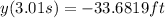
y(3.01 s) = -33.6819 ft

So, the average velocity will be

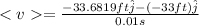
$<v> = \frac{-33.6819 ft \hat{j}- (-33 ft) \hat{j}}{0.01 s}$

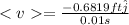
$<v> = \frac{-0.6819 ft \hat{j}}{0.01 s}$

$<v> = - 68.19 (ft)/(s) \hat{j}$

The minus sign is there cause the velocity is pointing downward.

After 0.005 s

After 0.005 s the position will be

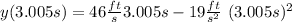
$y(3.005 s) = 46 (ft)/(s) 3.005 s - 19 (ft)/(s^2) \ (3.005 s)^2$

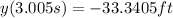
y(3.005 s) = -33.3405 ft

So, the average velocity will be

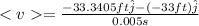
$<v> = \frac{-33.3405 ft \hat{j} - (-33 ft) \hat{j} }{0.005 s}$

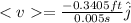
$<v> = (-0.3405 ft )/(0.005 s) \hat{j}$

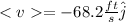
$<v> = - 68.2 (ft)/(s) \hat{j}$

After 0.002 s

After 0.002 s the position will be

$y(3.002 s) = 46 (ft)/(s) 3.002 s - 19 (ft)/(s^2) \ (3.002 s)^2$

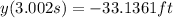
y(3.002 s) = -33.1361 ft

So, the average velocity will be

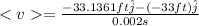
$<v> = \frac{-33.1361  ft \hat{j} - (-33 ft) \hat{j} }{0.002 s}$

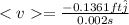
$<v> = \frac{-0.1361  ft \hat{j} }{0.002 s}$

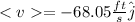
$<v> = - 68.05 (ft)/(s) \hat{j}$

After 0.001 s

After 0.001 s the position will be

$y(3.001 s) = 46 (ft)/(s) 3.001 s - 19 (ft)/(s^2) \ (3.001 s)^2$

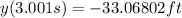
y(3.001 s) = -33.06802 ft

So, the average velocity will be

$<v> = \frac{-33.06802  ft  \hat{j} - (-33) ft \hat{j} }{0.001 s}$

$<v> = \frac{-0.06802  ft \hat{j} }{0.001 s}$

$<v> = - 68.02 (ft)/(s) \hat{j}$

Gavin Campbell answered Jul 2, 2020

by Gavin Campbell

8.2k points

← Prev Question Next Question →

Search Qammunity.org