Question

PLEASE HELP!!!!

Simplify the expression (x^4+4x^3-5x-20)÷(x+4) using synthetic division. After doing the synthetic division, which gives you just coefficients. Convert the coefficient quotient answer, into a polynomial with variable x and the correct exponent powers in it. Convert your coefficient answer into a polynomial.

Hint: remember to fill in any missing degree terms in your dividend with coefficients that are zero to represent missing place holders.

Answer 1

The answer to your question is: (x³ - 5) (x + 4)

Explanation:

x⁴ + 4x³ - 5x - 20 / x + 4 x = -4

1 4 0 -5 -20 -4

-4 0 0 +20

1 0 0 -5 0 = x³ - 5

Finally (x³ - 5) (x + 4) = x⁴ + 4x³ - 5x - 20

Answer 2

Explanation:

Given is an algebraic expression as

`(x^4+4x^3-5x-20)`

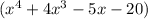
which is to be divided by
`x+4`

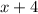
Method to be used: synthetic division

We write the coefficients of the dividend in descending order with 0 for non existing x term

So this would be as

1 4 0 -5 -20

Divisor equate to 0 to get

`x+4=0\\x=-4`

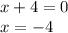
So we write -4 on the left side and do synthetic division. Synthetic division is writing I term as it is, and next step is to multiply the I term answer by -4 and write below II term. Now add the 2 terms in II column and continue this till the last term

-4 | 1 4 0 -5 -20

| -4 0 0 20

|__________________

1 0 0 -5 0=Remainder

Hence we find right most answer as remainder =0

Quotient is

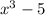`x^3-5`(writing from left most with powers of x in descending powers)