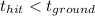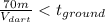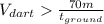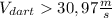Question

A sly 1.5-kg monkey and a jungle veterinarian with a blow-gun loaded with a tranquilizer dart are 25 m above the ground in trees 70 m apart. Just as the veterinarian shoots horizontally at the monkey, the monkey drops from the tree in a vain attempt to escape being hit. What must the minimum muzzle velocity of the dart be for the dart to hit the monkey before the mon- key reaches the ground?

Answer 1

minimum muzzle velocity of the dart:
`30,97 (m)/(s)`

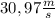
Step-by-step explanation:

Al t time t=0, the monkey drops and the dart is shot,

For the monkey the general position equation will be:

`y = y_(0) + V_(0)  t + (1)/(2) a t^(2)`

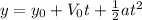
it starts from rest so
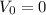`V_(0) = 0`, and the acceleration is
`a = -g`, so

(1)
`y = y_(0) - (1)/(2) g t^(2)`

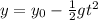
it will hit the ground when y = 0:

`0 = y_(0) - (1)/(2) g t_(ground)^(2)`

`t_(ground)^(2) = (2*y_(0))/(g)`

`t_(ground) = 2,26 s`

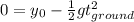
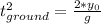
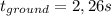
For the dart first we need to know the time when it reaches the monkey on the horizontal position, for this we have the equation:

`x = x_(0) + V_(dart)  t + (1)/(2) a t^(2)`

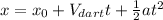
In this case, neglecting the air friction acceleration will be 0, and considering the origin on the gun
`x_(0) = 0`:

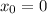(2)
`x = V_(dart)  t`

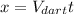
So the time when it hits the monkey would be when x = 70m:

(3)
`t_(hit) = (70m)/(V_(dart))`

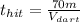
To hit the monkey before it reaches the ground it must be

`t_(hit) < t_(ground)`

`(70m)/(V_(dart)) < t_(ground)`

`V_(dart) > (70m)/(t_(ground))`

`V_(dart) > 30,97 (m)/(s)`